Trazado de curvas técnicas
En esta unidad Trazaremos
curvas técnicas (óvalos, ovoides y espirales), estos estas formados por arcos
de circunferencia tangentes.
1-
Ovalo: Curva cerrada y plana,
compuesta por arcos de circunferencia tangentes entre sí. Tiene dos ejes de simetría
perpendicular entre sí, y que se cortan en sus puntos medios.
Para trazar un ovalo dado el
eje Mayor
Primero trazamos
una recta siendo el inicio el punto A y el final el punto B el eje mayor.
Se divide en
tres partes iguales, quedando las divisiones de la siguiente manera: el punto
de inicio A, los puntos de intersección
M y N y el punto final B.
Con centro en la
intersección M y con radio en a A se describen la primera circunferencia.
Con centro en la
intersección N y con radio en a B se describen la segunda circunferencia.
Debemos de
trazar una diagonal que este entre el centro de M y N hasta los puntos de
encuentro donde se interceptan las circunferencias siendo estos los puntos O y
P.
Trazamos una
diagonal desde O pasando por M y N individualmente para obtener los puntos H y
G.
Trazamos una
diagonal desde P pasando por M y N individualmente para obtener los puntos E y
F.
Con centro en P
y radio en E se describe el arco E F.
Con centro en O
y radio en G se describe el arco G H.
Para trazar un ovalo dado el eje menor
Primero trazamos
una recta siendo el inicio el punto A y el final el punto B el eje mayor.
Y una diagonal
que pase por el centro de AB siendo el punto medio O y así se describe el eje menor CD.
En el punto
medio O de este eje y con radio igual a la mitad del mismo se describe una
circunferencia.
Los puntos donde
la circunferencia corta al eje mayor serán M y N.
Trazamos una
diagonal desde C pasando por M y se obtiene el Punto H.
Trazamos una
diagonal desde C pasando por N y se obtiene el Punto G.
Trazamos una
diagonal desde D pasando por M y se obtiene el Punto E.
Trazamos una
diagonal desde D pasando por N y se obtiene el Punto F.
Con centro en C
y radio en D se describe un arco de circunferencia GDH.
Con centro en D
y radio en C se describe un arco de circunferencia ECF.
Con centro en M
y radio E se describe el arco EAH y con centro en N y radio en F se describe el
arco FBG, con lo que se obtiene el ovalo buscado.
2- Ovoide:
Curva cerrada
y plana, compuesta por arcos de circunferencias tangentes entres si, dos arcos
de igual radio y otros de radio distinto, siendo el mayor de ellos una
semicircunferencia. Tiene un solo eje de simetría, que contiene a los centros
de los arcos desiguales.
Para trazar un ovoide dado el eje menor
Se
halla el punto medio O1 del
eje conocido y con centro en él se traza una circunferencia que tenga como
diámetro el propio eje.
Se
determina el punto O2 en la intersección de la circunferencia con la
mediatriz del eje AB.
Se
trazan las rectas que pasan por los extremos A y B del eje y el punto O2,
antes hallado.
Con
centro en A y en B se trazan dos arcos de radio igual al diámetro hasta que
corten a las prolongaciones de las rectas que pasan por los puntos A y B y O2.
Haciendo
centro en O2 y abriendo hasta las intersecciones de los arcos antes
descritos con las prolongaciones de las rectas, trazamos el arco que completa
el ovoide.
3-
Espiral: Es una curva plana, abierta,
generado por un punto P, situada en origen O de una semirrecta que se desplaza
sobre ella con un movimiento longitudinal, al mismo tiempo que la semirrecta
gira alrededor de O con un movimiento circular.
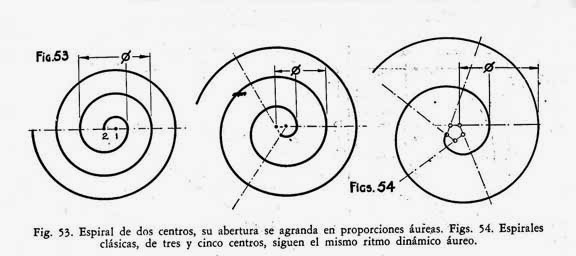
Para
trazar un espiral de dos centros y paso constante
Se determina la magnitud 2A del
paso constante y se halla su punto medio 1.
Con centro en el punto 1 se
traza una semicircunferencia de diámetro 2A.
Se continua la espiral trazando
el arco AC, con centro en el punto 2 y radio 2A.
Se describe después el arco CD,
volviendo al punto 1 como centro y abriendo el compas hasta el punto donde
termino el último arco trazado.
Para el arco DE se vuelve a
tomar el punto 2 como centro, así sucesivamente hasta completar tantos giros
como se quiera en el espiral.
No hay comentarios:
Publicar un comentario