Saludos a los que estan visitando mi pagina. En esta encomtraras los primeros paso de la algebra y tranformacion de plano.esperando que esta pequeña informacion les ayude.
lunes, 18 de noviembre de 2013
Unidades y presentacion asignatura
ASIGNATURA:
“ALGEBRA Y TRANSFORMACIONES DEL PLANO”
.CONTENIDOS:
>Movimiento del plano
>congruencia
>Simetria de deslizamiento la Rosa de los viento
>Simetria Central
>Simetria Axial
>simetria de Rotacion
>Homotecia
>Trazado de curvas tecnicas
>Isomeria
>Vistas auxiliares
OBJETIVO:
***DESARROLLAR TECNICAS DE APRENDIZAJES***
***PARA TRANSFORMACIONES DEL PLANO***.
Movimiento plano
Movimiento del plano.
Es
una transformación que no cambia la distancia y se denota con la letra M.
Teorema:
Teorema
1: El conjunto M de todos los movimientos, en relación a sus composiciones
forman un grupo de movimientos.
Teorema
2: Con el movimiento del plano tres puntos colineales se reflejan en tres puntos colineales
manteniendo la relación “entre”.
Teorema
3: Un movimiento del plano transforma la
circunferencia en otra del mismo radio.
Teorema
4: Un movimiento del plano transforma dos rectas paralelas en otras dos también
paralelas.
De
estos teoremas se desprenden importantes propiedades de las cuales enumeramos
algunas:
-
El
movimiento del plano transforman una recta en otra recta.
-
El
movimiento del plano transforma un semiplano con frontera a, en el semiplano
con frontera , donde a es la imagen de la recta.
-
El
movimiento del plano guarda la relación “estar entre”.
-
El
movimiento transforma el segmento AB en el segmento A-B,
donde A y B son las imágenes de los puntos A,B. El
punto medio del segmento AB se transforma en el punto medio del segmento A-B.
-
El
movimiento transforma un rayo en otro rayo, un ángulo en otro ángulo igual al
primero.
-
El
movimiento transforma las rectas perpendiculares en rectas perpendiculares.
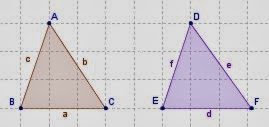
Congruencia
En matemáticas, dos figuras de puntos son congruentes si tienen los lados iguales y el mismo tamaño (o también, están relacionados por un movimiento) si existe una isometría que los relaciona: una transformación que es de translaciones, rotaciones y reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.
Simetria de Deslizamiento vectores--Rosa de los viento
El desplazamiento
es el vector que define la posición de un punto o partícula en relación
a un origen A con respecto a una posición B. El vector se extiende desde el
punto de referencia hasta la posición final. Cuando se habla del desplazamiento
de un cuerpo en el espacio solo importa la posición inicial del cuerpo y la
posición final, ya que la trayectoria que describe el cuerpo no es de importancia si
igual a la final.
Roza de los vientos
Roza de los vientos
Una rosa
de los vientos es un círculo que tiene marcados alrededor los rumbos en que
se divide la circunferencia del horizonte. En las cartas de navegación se
representa por 32 rombos (deformados) unidos por un extremo mientras el otro
señala el rumbo sobre el círculo del horizonte. Sobre el mismo se sitúa la flor
de lis con la que suelen representar el Norte que se documenta a partir del siglo
XV.
También puede ser un diagrama que representa la intensidad media del viento en diferentes sectores en los que divide el círculo del horizonte.
Simetria central
a) El punto y su imagen estén a igual distancia de un punto llamado centro de simetría.
b) El punto, su imagen y el centro de simetría pertenezcan a una misma recta.
Según estas definiciones, con una simetría central se obtiene la misma figura con una rotación de 180 grados.
Una simetría central, de centro el punto O, es un movimiento del plano con el que a cada punto P del plano le hace corresponder otro punto P', siendo O el punto medio del segmento de extremos P y P'
simetria axial
Decimos que una figura plana tiene simetría
axial cuando podemos trazar una recta (llamada eje de simetría) que
divida en dos partes la figura, de manera que si plegamos el plano por ese eje las dos partes coinciden.
Observa que una parte "se refleja" en el eje para formar la otra, como si el eje
actuase de espejo.
En esta actividad podrás dibujar figuras que tengan simetría
axial, a partir del eje de simetría que la aplicación te mostrará. Solo tienes
que mover el punto P (no lo confundas con P').
Rotacion
Decimos que una figura plana tiene simetría
rotacional cuando podemos encontrar un centro (llamado centro de rotación)
de manera que si giramos la figura completa un cierto ángulo (mayor o
igual a 0º y menor que 360º), la figura rotada coincide con la figura original.
Cuando un figura tiene simetría rotacional, a cada
punto le corresponden otro punto (que se llama "punto rotado" o "imagen") a
la misma distancia del centro, de forma que el ángulo que forman ambos con el
centro de rotación es siempre el mismo. El número de veces que se puede hacer
coincidir la imagen rotada con figura original se llama orden de la
rotación.
Cualquier figura tiene al menos una simetría
rotacional de orden 1 alrededor de cualquier punto que elijamos como centro,
pues basta elegir como ángulo de rotación 0º (es decir, dejar la figura como
está).
En esta actividad deberás crear figuras que tengan simetría
rotacional, a partir del centro de rotación que la aplicación te mostrará. Podrás elegir
el orden de rotación de la figura y deberás calcular, según sea el orden
elegido, el ángulo de rotación correspondiente.
Homotecia
Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. En general una homotecia de razón (λ) diferente de 1 deja un único punto fijo, llamado centro de la transformación.
El tamaño de una homotesia de pendera si el numero es mayor o menor. un ejemplo puede ser 1.5 este sera mayor y 0.5 este sera menor.
Trasado de curbas tecnicas
Trazado de curvas técnicas
En esta unidad Trazaremos
curvas técnicas (óvalos, ovoides y espirales), estos estas formados por arcos
de circunferencia tangentes.
1-
Ovalo: Curva cerrada y plana,
compuesta por arcos de circunferencia tangentes entre sí. Tiene dos ejes de simetría
perpendicular entre sí, y que se cortan en sus puntos medios.
Para trazar un ovalo dado el
eje Mayor
Primero trazamos
una recta siendo el inicio el punto A y el final el punto B el eje mayor.
Se divide en
tres partes iguales, quedando las divisiones de la siguiente manera: el punto
de inicio A, los puntos de intersección
M y N y el punto final B.
Con centro en la
intersección M y con radio en a A se describen la primera circunferencia.
Con centro en la
intersección N y con radio en a B se describen la segunda circunferencia.
Debemos de
trazar una diagonal que este entre el centro de M y N hasta los puntos de
encuentro donde se interceptan las circunferencias siendo estos los puntos O y
P.
Trazamos una
diagonal desde O pasando por M y N individualmente para obtener los puntos H y
G.
Trazamos una
diagonal desde P pasando por M y N individualmente para obtener los puntos E y
F.
Con centro en P
y radio en E se describe el arco E F.
Con centro en O
y radio en G se describe el arco G H.
Para trazar un ovalo dado el eje menor
Primero trazamos
una recta siendo el inicio el punto A y el final el punto B el eje mayor.
Y una diagonal
que pase por el centro de AB siendo el punto medio O y así se describe el eje menor CD.
En el punto
medio O de este eje y con radio igual a la mitad del mismo se describe una
circunferencia.
Los puntos donde
la circunferencia corta al eje mayor serán M y N.
Trazamos una
diagonal desde C pasando por M y se obtiene el Punto H.
Trazamos una
diagonal desde C pasando por N y se obtiene el Punto G.
Trazamos una
diagonal desde D pasando por M y se obtiene el Punto E.
Trazamos una
diagonal desde D pasando por N y se obtiene el Punto F.
Con centro en C
y radio en D se describe un arco de circunferencia GDH.
Con centro en D
y radio en C se describe un arco de circunferencia ECF.
Con centro en M
y radio E se describe el arco EAH y con centro en N y radio en F se describe el
arco FBG, con lo que se obtiene el ovalo buscado.
2- Ovoide:
Curva cerrada
y plana, compuesta por arcos de circunferencias tangentes entres si, dos arcos
de igual radio y otros de radio distinto, siendo el mayor de ellos una
semicircunferencia. Tiene un solo eje de simetría, que contiene a los centros
de los arcos desiguales.
Para trazar un ovoide dado el eje menor
Se
halla el punto medio O1 del
eje conocido y con centro en él se traza una circunferencia que tenga como
diámetro el propio eje.
Se
determina el punto O2 en la intersección de la circunferencia con la
mediatriz del eje AB.
Se
trazan las rectas que pasan por los extremos A y B del eje y el punto O2,
antes hallado.
Con
centro en A y en B se trazan dos arcos de radio igual al diámetro hasta que
corten a las prolongaciones de las rectas que pasan por los puntos A y B y O2.
Haciendo
centro en O2 y abriendo hasta las intersecciones de los arcos antes
descritos con las prolongaciones de las rectas, trazamos el arco que completa
el ovoide.
3-
Espiral: Es una curva plana, abierta,
generado por un punto P, situada en origen O de una semirrecta que se desplaza
sobre ella con un movimiento longitudinal, al mismo tiempo que la semirrecta
gira alrededor de O con un movimiento circular.
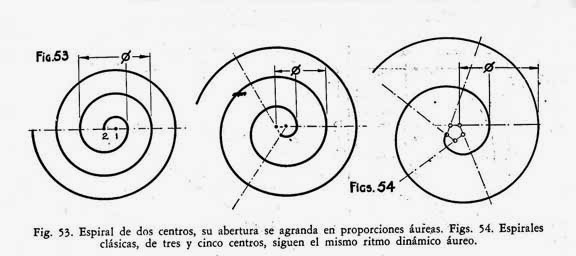
Para
trazar un espiral de dos centros y paso constante
Se determina la magnitud 2A del
paso constante y se halla su punto medio 1.
Con centro en el punto 1 se
traza una semicircunferencia de diámetro 2A.
Se continua la espiral trazando
el arco AC, con centro en el punto 2 y radio 2A.
Se describe después el arco CD,
volviendo al punto 1 como centro y abriendo el compas hasta el punto donde
termino el último arco trazado.
Para el arco DE se vuelve a
tomar el punto 2 como centro, así sucesivamente hasta completar tantos giros
como se quiera en el espiral.
Isometrica
isométrica:
es una técnica de representación gráfica de un objeto tridimensional en dos dimensiones,
donde los tres ejes coordenados ortogonales al proyectarse forma ángulos
iguales de 1200 cada uno sobre el plano
Vistas auxiliares
Vista auxiliar
que se hace tomando una dirección de observación que no es perpendicular al plano horizontal, vertical o de perfil.
Generalmente la vista auxiliar se toma perpendicular a una de las caras del objeto que no está paralela a uno de los planos de proyección.
Su utilidad es la de evitar las deformaciones de aquellas partes oblicuas a los planos de proyección.
Cuando se dibujan vistas auxiliares se suprimen las partes deformadas, representadas en estas, de las otras vistas, incluyéndose una línea de rotura o línea de trazo y punto en su lugar.
Suscribirse a:
Entradas (Atom)